König's theorem (graph theory)
In the mathematical area of graph theory, König's theorem, proved by Dénes Kőnig in 1931, describes an equivalence between the maximum matching problem and the minimum vertex cover problem in bipartite graphs. It was discovered independently, also in 1931, by Jenő Egerváry in the more general case of weighted graphs.
Contents |
Setting
A graph is bipartite if its vertices can be partitioned into two sets such that each edge has one endpoint in each set. A vertex cover in a graph is a set of vertices that includes at least one endpoint of each edge, and a vertex cover is minimum if no other vertex cover has fewer vertices. A matching in a graph is a set of edges no two of which share an endpoint, and a matching is maximum if no other matching has more edges. König's theorem states that, in any bipartite graph, the number of edges in a maximum matching is equal to the number of vertices in a minimum vertex cover.
For graphs that are not bipartite, the maximum matching and minimum vertex cover problems are very different in complexity: maximum matchings can be found in polynomial time for any graph, while minimum vertex cover is NP-complete. The complement of a vertex cover in any graph is an independent set, so a minimum vertex cover is complementary to a maximum independent set; finding maximum independent sets is another NP-complete problem. The equivalence between matching and covering articulated in König's theorem allows minimum vertex covers and maximum independent sets to be computed in polynomial time for bipartite graphs, despite the NP-completeness of these problems for more general graph families.
König's theorem is equivalent to numerous other min-max theorems in graph theory and combinatorics, such as Hall's marriage theorem and Dilworth's theorem. Since bipartite matching is a special case of maximum flow, the theorem also results from the max flow min cut theorem.
König's theorem is named after the Hungarian mathematician Dénes Kőnig. Kőnig had announced in 1914 and published in 1916 the results that every regular bipartite graph has a perfect matching,[1] and more generally that the chromatic index of any bipartite graph (that is, the minimum number of matchings into which it can be partitioned) equals its maximum degree[2] – the latter statement is known as König's Line Coloring Theorem.[3] However, Bondy and Murty (1976) attribute König's theorem itself to a later paper of Kőnig (1931). According to Biggs et al., Kőnig attributed the idea of studying matchings in bipartite graphs to his father, mathematician Gyula Kőnig. Note that, although Kőnig's name is properly spelled with a double acute accent, the theorem named after him is customarily spelled with an umlaut.
Statement of the theorem
In any bipartite graph, the number of edges in a maximum matching equals the number of vertices in a minimum vertex cover.
Example
The bipartite graph shown in the above illustration has 14 vertices; a matching with six edges is shown in blue, and a vertex cover with six vertices is shown in red. There can be no smaller vertex cover, because any vertex cover has to include at least one endpoint of each matched edge, so this is a minimum vertex cover. Similarly, there can be no larger matching, because any matched edge has to include at least one endpoint in the vertex cover, so this is a maximum matching. König's theorem states that the equality between the sizes of the matching and the cover (in this example, both numbers are six) applies more generally to any bipartite graph.
Algorithm
Consider a bipartite graph where the vertices are partitioned into left ( ) and right (
) and right ( ) sets. Suppose there is a maximum matching which partitions the edges into those used in the matching (
) sets. Suppose there is a maximum matching which partitions the edges into those used in the matching (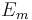 ) and those not (
) and those not (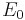 ). Let
). Let  consist of all unmatched vertices from L, as well as all vertices reachable from those by going left-to-right along edges from
consist of all unmatched vertices from L, as well as all vertices reachable from those by going left-to-right along edges from 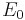 and right-to-left along edges from
and right-to-left along edges from 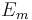 . This essentially means that for each unmatched vertex in L, we add into T all vertices that occur in a path alternating between edges from
. This essentially means that for each unmatched vertex in L, we add into T all vertices that occur in a path alternating between edges from 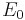 and
and 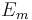 .
.
Then 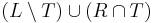 is a minimum vertex cover. Intuitively, vertices in
is a minimum vertex cover. Intuitively, vertices in  are added if they are in
are added if they are in  and subtracted if they are in
and subtracted if they are in  to obtain the minimum vertex cover. Thus, the Hopcroft–Karp algorithm for finding maximum matchings in bipartite graphs may also be used to solve the vertex cover problem efficiently in these graphs.
to obtain the minimum vertex cover. Thus, the Hopcroft–Karp algorithm for finding maximum matchings in bipartite graphs may also be used to solve the vertex cover problem efficiently in these graphs.
Proof
Suppose that G=(V,E) is a bipartite graph, where V = A ∪ B. Let M be a matching for G.
We must show either G has a vertex cover C of size |M|, or M is not a maximum matching.
First, if M is a perfect matching, then M is maximum. In this case, every edge is incident to exactly one vertex on either side, so any partition of G is a vertex cover of size |M| and we are done.
Otherwise, use an alternating path argument. An alternating path is a path where the edges alternate between M and E \ M. Partition the vertices of G into subsets Si as follows. Let S0 consist of all vertices unmatched by M. For integer j ≥ 0, let S2j+1 be the set of vertices that:
- Are adjacent to vertices in S2j via some edge e ∈ E \ M.
- Have not been included in any previously-defined set Sk, where k < j.
Each vertex v ∈ S2j+1 must be adjacent to another vertex u via an edge e ∈ M (otherwise, v is unmatched by M and would have been placed in S0). If the u has not yet been included in a set Si, insert u in S2j+2. If there are no vertices adjacent to S2j, arbitrarily pick an unused vertex and continue in S2j+1.
The illustration is an isomorphic partitioning of the example graph and its matching.
Each vertex in Si has an edge to a vertex in Si−1. An alternating path can be formed from a given vertex, going up one level at a time, ending either at an unmatched vertex or at a level containing a single (matched) vertex.
If there exists any matched edge uv between two vertices u and v in the same odd-level subset S2j+1, the two alternating paths for u and v can be connected via edge uv. There cannot be any edges in M between vertices in an even level subset S2j, because each of the vertices is connected by its single matched edge to a vertex in the previous level. This path cannot have any repeated vertices since G is bipartite, so the start and end vertices must be distinct.
Now confirm that M is a maximum matching:
- If both the start and end vertices of an alternating path are unmatched, the path contains one more edge in M than in E \ M. Swap the matched and unmatched edges. This gives a larger M', so M cannot be a maximum matching.
- If there exists an unmatched edge uv between two vertices u and v in the same even-level subset S2j, uv can be inserted in M to create a larger M' because u and v were unmatched. Then M is also not a maximum matching.
Thus, if M is maximum, each edge in M has a single endpoint in an odd-level subsets S2j+1, and each edge in E \ M has at least one endpoint in an odd-level subset S2j+1. The union of the odd-level subsets forms a vertex cover of size |M|. Since no smaller set of vertices could cover every edge in M, it must be a minimum vertex cover.
Therefore, a bipartite graph G with maximum matching M and minimum vertex cover C satisfies |M| = |C|.
Connections with perfect graphs
A graph is said to be perfect if, in every induced subgraph, the chromatic number equals the size of the largest clique. Any bipartite graph is perfect, because each of its subgraphs is either bipartite or independent; in a bipartite graph that is not independent the chromatic number and the size of the largest clique are both two while in an independent set the chromatic number and clique number are both one.
A graph is perfect if and only if its complement is perfect (Lovász 1972), and König's theorem can be seen as equivalent to the statement that the complement of a bipartite graph is perfect. For, each color class in a coloring of the complement of a bipartite graph is of size at most 2 and the classes of size 2 form a matching, a clique in the complement of a graph G is an independent set in G, and as we have already described an independent set in a bipartite graph G is a complement of a vertex cover in G. Thus, any matching M in a bipartite graph G with n vertices corresponds to a coloring of the complement of G with n-|M| colors, which by the perfection of complements of bipartite graphs corresponds to an independent set in G with n-|M| vertices, which corresponds to a vertex cover of G with M vertices. Conversely, König's theorem proves the perfection of the complements of bipartite graphs, a result proven in a more explicit form by Gallai (1958).
One can also connect König's Line Coloring Theorem to a different class of perfect graphs, the line graphs of bipartite graphs. If G is a graph, the line graph L(G) has a vertex for each edge of G, and an edge for each pair of adjacent edges in G. Thus, the chromatic number of L(G) equals the chromatic index of G. If G is bipartite, the cliques in L(G) are exactly the sets of edges in G sharing a common endpoint. Now König's Line Coloring Theorem, stating that the chromatic index equals the maximum vertex degree in any bipartite graph, can be interpreted as stating that the line graph of a bipartite graph is perfect.
Since line graphs of bipartite graphs are perfect, the complements of line graphs of bipartite graphs are also perfect. A clique in the complement of the line graph of G is just a matching in G. And a coloring in the complement of the line graph of G, when G is bipartite, is a partition of the edges of G into subsets of edges sharing a common endpoint; the endpoints shared by each of these subsets form a vertex cover for G. Therefore, König's theorem itself can also be interpreted as stating that the complements of line graphs of bipartite graphs are perfect.
Notes
- ^ In a poster displayed at the 1998 International Congress of Mathematicians in Berlin and again at the Bled'07 International Conference on Graph Theory, Harald Gropp has pointed out that the same result already appears in the language of configurations in the 1894 thesis of Ernst Steinitz.
- ^ Biggs et al. (1976).
- ^ Lovász and Plummer (1986), Theorem 1.4.17, pp.37ff.
References
- Biggs, N. L.; Lloyd, E. K.; Wilson, R. J. (1976). Graph Theory 1736–1936. Oxford University Press. pp. 203–207. ISBN 0-19-853916-9.
- Bondy, J. A.; Murty, U. S. R. (1976). Graph Theory with Applications. North Holland. p. 74. ISBN 0-444-19451-7.
- Gallai, Tibor (1958). "Maximum-minimum Sätze über Graphen". Acta Math. Acad. Sci. Hungar. 9 (3-4): 395–434. doi:10.1007/BF02020271. MR0124238.
- Kőnig, Dénes (1916). "Gráfok és alkalmazásuk a determinánsok és a halmazok elméletére". Matematikai és Természettudományi Értesítő 34: 104–119.
- Kőnig, Dénes (1931). "Gráfok és mátrixok". Matematikai és Fizikai Lapok 38: 116–119.
- Lovász, László; M.D. Plummer (1986). Matching Theory. North-Holland. ISBN 0444879161.
- Lovász, László (1972). "Normal hypergraphs and the perfect graph conjecture". Discrete Mathematics 2 (3): 253–267. doi:10.1016/0012-365X(72)90006-4. MR0302480.